Najistejšou všeobecnou charakteristikou európskej filozofickej tradície je to, že pozostáva zo série poznámok k Platónovi.
Alfred North Whitehead
Väčšina filozofov si myslí, že paradox sa týka úsudku, ktorý vedie od prijateľných predpokladov k neprijateľnému záveru použitím prijateľného zdôvodnenia [1] . Ja už som ale namietol, že táto definícia je príliš úzka; nezahŕňa totiž paradoxy súvisiace s vnímaním z prvej kapitoly a nezmyselné paradoxy z tretej kapitoly. Teraz chcem kritizovať tento prevládajúci názor aj ako príliš široký. Moje protipríklady využívajú paradox z úvodu a „paradoxy striktnej implikácie“.
Pravdovravnosť
Platónovo skutočné meno bolo Aristokles. „Platón“ bola jeho prezývka. Znamenala niečo ako „širokoplecnatý“. Meno bolo výstižné vzhľadom na Platónovu mohutnú postavu pripomínajúcu zápasníka.
Nebolo ale Platónovo pôvodné meno ešte výstižnejšie? Niekto je dobre pomenovaný, ak ho predikát zodpovedajúci jeho menu výstižne popisuje. Profesor Rozvážny je dobre pomenovaný, pretože je rozvážny. Profesor Pochmúrny je zle pomenovaný, pretože nie je pochmúrny. Aristokles znamená dobre pomenovaný. [2] Takže problémom je, či Dobrepomenovaný je dobre pomenovaný.
Do dilemy by sme sa dostali vtedy, keby sa Platón namiesto toho volal Zlepomenovaný (Geach 1948). Zlepomenovaný je buď dobre pomenovaný alebo zle pomenovaný. Ak Zlepomenovaný je zle pomenovaný, tak predikát zodpovedajúci jeho menu ho popisuje výstižne. Takže ak je zle pomenovaný, potom z toho vyplýva, že je dobre pomenovaný. Ak je ale Zlepomenovaný dobre pomenovaný, tak predikát zodpovedajúci jeho menu sa naňho nevzťahuje.
Dilema zlého pomenovania je jednou z verzií paradoxu klamára: K: Tvrdenie K je nepravdivé. Ak K je pravdivé, tak potom – pretože hovorí, že je nepravdivé – musí byť nepravdivé. Ale ak je tvrdenie K nepravdivé, potom sa veci majú tak, ako hovorí K – takže v takom prípade je napokon K pravdivé. K je paradoxné, pretože nie je možné presne určiť jeho pravdivostnú hodnotu.
Opačné zadanie robí paradoxným aj pravdovravný výrok: P: Tvrdenie P je pravdivé. P je paradoxné, pretože môžeme tvrdeniu P konzistentne [3] priradiť ktorúkoľvek pravdivostnú hodnotu. Keďže niet ničoho, na základe čoho by bolo možné priradiť pravdivostnú hodnotu, P by bolo pravdivé alebo nepravdivé bez toho, aby ho niečo robilo pravdivým alebo nepravdivým.
Väčšina logikov na to reaguje tak, že nepovažujú tvrdenie P ani za pravdivé ani za nepravdivé. To je založené na názore, že uvedená veta je bezobsažná. Ale ak P nie je ani pravdivé ani nepravdivé, tak sa zdá, že P falošne predstiera svoju pravdivosť.
„Dobrepomenovaný je dobre pomenovaný“ je inou verziou pravdovravného paradoxu. Bez toho, aby sme si odporovali, môžeme povedať, že veta „Dobrepomenovaný je dobre pomenovaný“ je pravdivá, ale rovnako konzistentne môžeme povedať aj to, že je nepravdivá. Ak usúdime, že nemá žiadnu pravdivostnú hodnotu, tak veta „Dobrepomenovaný je dobre pomenovaný“ sa zdá byť nepravdivá, pretože slovné spojenie dobre pomenovaný nepopisuje pravdivo Dobrepomenovaného. Ale ak spojenie dobre pomenovaný výstižne popisuje Dobrepomenovaného, aká je to vlastnosť, čo ho tak výstižne popisuje? Je to práve vlastnosť byť dobre pomenovaným?
Je Aristokles Aristoklom? Platón túto filozofickú otázku prepásol. Aká premrhaná príležitosť! Filozofia sa mohla stať sériou poznámok k Aristoklovi.
Paradox z úvodu
Vedel Platón o paradoxe klamára? Legenda o Epimenidovi kolovala už stovky rokov pred Platónovým narodením. Platón necháva Sokrata vzniesť námietku proti Protagorovi, ktorá má blízko k paradoxu klamára. Protagorov slogan „Človek je mierou všetkých vecí“ je predstavovaný tak, akoby z neho vyplývalo, že všetky presvedčenia [4] sú pravdivé: Čo sa každému zdá, pre toho, komu sa zdá, aj to skutočne je. [5] Na vyvrátenie Protagora potreboval Sokrates takú kritiku, ktorá by bola použiteľná na systém presvedčení jednotlivca. Možnosť jej zahájenia videl vo fakte, že každá osoba má nejaké presvedčenia o svojich presvedčeniach:
…niet človeka, ktorý by sa nedomnieval, že je v niektorých veciach múdrejší než ostatní, v druhých zasa sú iní múdrejší ako on. A v najväčších nebezpečenstvách, kedykoľvek sa ľudia na vojenských výpravách, alebo v chorobách, alebo na mori, dostávajú do ťažkej situácie, obracajú sa na tých, ktorí sú práve v tom čase ich vodcami, ako na bohov a od nich čakajú záchranu, i keď tí sa od nich nelíšia ničím iným, iba vedením. A v celej ľudskej spoločnosti je plno takých, ktorí hľadajú učiteľov a vodcov i pre seba i pre iné živé tvory a pre výkony, a aj takých, ktorí sa domnievajú, že sú schopní vyučovať a že sú schopní vládnuť.(Teaitetos 170 A-B) [6]
Uvažujme o niekom, kto sa domnieva, že aspoň jedno z jeho presvedčení je nepravdivé. Z Protagorovho princípu, že všetky presvedčenia sú pravdivé, vyplýva, že tvrdenie „Aspoň jedno z mojich presvedčení je nepravdivé“ je pravdivé pre tohto skromného jedinca. Keď teda aplikujeme tvrdenie „Všetky presvedčenia sú pravdivé pre toho, kto ich zastáva“ na onoho skromného vyznavača, dostávame: „Nie všetky presvedčenia sú pravdivé pre toho, kto ich zastáva.“ Keďže protagorovský relativizmus implikuje svoju vlastnú nepravdivosť, znamená to, že protagorovský relativizmus je nepravdivý.
Sokratova námietka voči Protagorovi pripomína D. C. Mackinsonov (1965) paradox z úvodu. V úvode knihy, ktorú teraz čítate, sa ospravedlňujem za omyly, ktoré určite budú v texte. Toto uznanie vlastnej omylnosti je prejavom zdravého rozumu. A predsa spôsobuje, že je nemožné, aby všetky moje presvedčenia boli pravdivé. Ak presvedčenie vyjadrené v úvode je pravdivé, tak jedno z presvedčení v texte je nepravdivé. Ak všetky presvedčenia v texte sú pravdivé, tak presvedčenie v úvode je nepravdivé. Tak či onak, niektoré z mojich presvedčení je nepravdivé.
Hoci paradox z úvodu narušuje Protagorov relativizmus, podkopáva tiež Platónov predpoklad, že z racionality vyplýva konzistencia. Keďže je nemožné, aby všetky moje presvedčenia týkajúce sa tejto knihy boli pravdivé, ako celok sú nekonzistentné. A predsa, presvedčenie, ktoré som vyjadril v úvode, je racionálne.
Zaiste, tento stupeň intelektuálnej pokory je intelektuálne povinný. Poznaj sám seba! Keby som prestal veriť, že niektoré z mojich presvedčení vyjadrené v tomto texte sú nepravdivé, bol by som namysleným učencom.
Úsudky typu hromada
Okrem toho, že som skromný v otázke toho, či moje presvedčenia sú pravdivé, mal by som byť skromný aj v otázke toho, či všetky moje presvedčenia sú konzistentné. Čím viac poviem, tým mám viac príležitostí, aby som si protirečil. V tejto knihe hovorím veľmi veľa, a tak sa domnievam, že tvrdenia v tomto texte (dokonca aj okrem tých z úvodu) sú ako celok nekonzistentné.
Vezmime prvých 10 001 tvrdení, ktoré zastávam v tejto knihe. Domnievam sa, že akékoľvek spojenie 10 000 z nich je nekonzistentné. Zvážme teraz ktorýkoľvek úsudok, ktorý obsahuje 10 000 z mojich 10 001 tvrdení ako predpoklady a negáciu zvyšného tvrdenia ako záver. Tento úsudok typu hromada by vyhovoval R. M. Sainsburyho definícii paradoxu:
Paradoxu rozumiem takto: očividne neprijateľný záver získaný očividne prijateľným zdôvodnením z očividne prijateľných predpokladov. Zdanie musí klamať, pretože prijateľné nemôže prostredníctvom prijateľných krokov viesť k neprijateľnému. Takže vo všeobecnosti máme takúto voľbu: buď záver v skutočnosti nie je neprijateľný, alebo či už východisko alebo zdôvodnenie obsahujú nejakú nenápadnú trhlinu. (Sainsbury 1995, 1)
Záver úsudku typu hromada je pre mňa neprijateľný, pretože vo svojej knihe úprimne trvám na jeho negácii. Každý predpoklad z uvedenej hromady je prijateľný, pretože vo svojej knihe na ňom úprimne trvám. Zdôvodnenie v úsudku typu hromada je pre mňa prijateľné, pretože si myslím, že úsudok je deduktívne platný [7] : Akýkoľvek úsudok s predpokladmi, ktoré sú ako celok nekonzistentné, je automaticky platný. Tento princíp vyplýva z definície platnosti: úsudok je platný, ak neexistuje možnosť, že by všetky predpoklady boli pravdivé a záver nepravdivý.
Úsudok je zdravý (sound) ak je platný (valid) a pritom sú jeho predpoklady pravdivé. Keďže logici nemajú žiadne zvláštne vedomosti o pravdivosti predpokladov, zameriavajú sa na platnosť. S potešením schvaľujú také smiešne úsudky ako „Všetky korytnačky patria do radu Testudines. Platón je korytnačka. Preto Platón patrí do radu Testudines.“ Ak obidva predpoklady boli pravdivé, tak aj záver by mal byť pravdivý. Platnosť je iba podmienenou garanciou pravdivého záveru. Ak nie je možné dosiahnuť, aby všetky predpoklady boli pravdivé, potom taká garancia nič nezaručuje.
Euklidovi žiaci v Megare (najznámejší Filón) [8] razili logickú náuku, že oznamovací kondicionál [9] „Ak p, tak q“ je nepravdivý iba vtedy, keď antecedent p je pravdivý a konzekvent q nepravdivý. Z toho vyplývajú dva „paradoxy materiálnej implikácie“. Jeho negatívna verzia hovorí, že akýkoľvek oznamovací kondicionál s nepravdivým antecedentom je pravdivý. Napríklad veta „Ak Sokrates bol na mesiaci, tak Platón bol na slnku“ z toho vychádza ako pravdivá. Pozitívna verzia hovorí, že akýkoľvek oznamovací kondicionál s pravdivým konzekventom je pravdivý. Teda veta „Ak Sokrates navštívil Atlantídu, tak Platón navštívil Megaru“ z toho vychádza ako pravdivá.
Niektorí logici zjemňujú tento úder zdôrazňovaním toho, že striktný kondicionál má formu: „Nutne platí, akp, tak q.“ Tieto kondicionály sa nestávajú automaticky pravdivými tým, že antecedent je nepravdivý alebo konzekvent pravdivý. Avšak neskorší logici objavili „paradoxy striktnej implikácie“: striktný kondicionál sa stáva automaticky pravdivým vďaka nutnej nepravdivosti svojho antecedentu alebo nutnej pravdivosti svojho konzekventu. Mnoho menších paradoxov krúži okolo paradoxov striktnej implikácie. Mojím obľúbeným je dôkaz Jaakko Hintikku o tom, že je nemorálne robiť to, čo nemožné: Človek nikdy nesmie robiť niečo, čo by spôsobilo skazu ľudskej rasy. Človek nemôže vykonať nemožný skutok bez toho, aby nezničil ľudskú rasu. Preto človek nesmie robiť to, čo je nemožné.
Úsudok je platný, ak zo spojenia jeho predpokladov striktne vyplýva [10] záver. Teda paradoxy striktnej implikácie ovplyvňujú niektoré verdikty týkajúce sa platnosti. Ak je záver úsudku nutne pravdivý, tak úsudok je automaticky platný. Ak sú všetky predpoklady pravdivé, potom úsudok bude aj zdravý. Toto je základom niektorých rafinovaných dôkazov Božej existencie. Stredovekí logici sa domnievali, že veta „Boh existuje“ je nutnou pravdou, a tak zmätočne považovali vetu „Platón filozofoval, preto Boh existuje“ za zdravý úsudok. Zbožný matematický génius Leonard Euler (1707-1783) vyrukoval s týmto logickým trikom na francúzskeho ateistu Denisa Diderota. Euler ho oslovil pred dvorom Kataríny Veľkej a slávnostne povedal: „Pane, (a + bn) / n = x, preto Boh existuje. Odpovedzte!“ Keďže Diderot sa v matematike veľmi nevyznal, nevedel, čo na to povedať. V St. Peterburgu ho vysmiali, a tak sa poponáhľal späť Francúzska.
Vyznavač klasickej logiky môže súčasne považovať úsudok za zdravý a pritom aj za pozitívny príklad paradoxu striktnej implikácie. Napríklad stredovekí logici pokladali úsudok „Platón filozofoval, preto Boh existuje“ za paradoxný, hoci súhlasili s tým, že je to zdravý (sound) dôkaz. Paradox môže spočívať viac v tom, ako niečo dokazujeme, než v tom, čo dokazujeme. Toto je ťažko stráviteľné pre tých, ktorí hovoria, že všetky paradoxy vystupujú vo forme neprijateľných záverov. Ich ponímanie je príliš úzke.
Úsudky typu hromada využívajú dôsledky negatívneho paradoxu striktnej implikácie: Akýkoľvek úsudok s predpokladmi, ktorých spojením vzíde nutná nepravda, musí byť pravdivým úsudkom. Keď je úsudok typu hromada prispôsobený systému presvedčení skromného klasického logika, ten zdôvodnenie akceptuje, pretože si myslí, že spojenie predpokladov je nutne nepravdivé. (Či je aj skutočne nepravdivé, to nie je dôležité pre účely protipríkladu.)
Ak úsudky typu hromada kvalifikujeme ako paradoxy, potom negácia ktoréhokoľvek môjho presvedčenia je paradoxom. Je to preto, že takto by bola neprijateľným záverom podopretým úsudkom, ktorého predpoklady aj zdôvodnenie (ja osobne) akceptujem.
Samozrejme, každý úsudok typu hromada považujem za nezdravý. Ale to je pre paradoxy bežné. Závery Zenónových úsudkov sú očividne nepravdivé, takže jeho úsudky musia byť nezdravé. Ale táto zrejmá nezdravosť mi nebráni v tom, aby som Zenónove závery klasifikoval ako paradoxy.
Nemôžeme vylúčiť úsudky typu hromada tak, že budeme požadovať, aby paradoxy boli krátkymiúsudkami. Úsudok Sorites [11] môže mať aj 10 000 predpokladov. Existujú aj paradoxné pravdy ako veta o neúplnosti Kurta Gödela, ktorej dôkaz zaberie celý semester. Gödelov dôkaz je zdĺhavý skôr kvôli Gödelovej obozretnosti než kvôli nejakej sofistike.
Pre mnohých z nás je možné uviesť aj krátke úsudky typu hromada. Paradoxy presvedčili mnohých filozofov, že majú malú množinu presvedčení, ktoré sú jednotlivo vierohodné a pritom ako celok konzistentné. Ak sú tieto presvedčenia použité ako predpoklady úsudku a negácia niektorého iného presvedčenia je použitá ako záver, potom tento záver bude vyhovovať Sainsburyho definícii paradoxu. A tak z jedného rýdzeho paradoxu môžeme nechať vyrásť toľko krátkych úsudkov typu hromada, koľko máme presvedčení.
Myslím si, že skutočný rozdiel medzi Zenónovými paradoxmi a úsudkami typu hromada je ten, že úsudky typu hromada môžu byť diagnostikované ako nezdravé bez porušenia sokratovského prikázania: Nespoliehaj sa na nevierohodnosť záveru, keď vysvetľuješ, prečo je úsudok nesprávny. Na tejto požiadavke trvám vtedy, keď vyvodzujem nezdravosť úsudku typu hromada priamo z nekonzistentnosti jeho predpokladov.
Racionálny základ sokratovského prikázania spočíva v tom, že Sokrates chcel používať úsudok ako metódu objavovania. Nesúhlasil s Mysónom, ktorý „hovorieval, že by sme nemali skúmať fakty vo svetle argumentov, ale argumenty vo svetle faktov“. (Diogenes 1925, I, 107-108) Sokrates nepovažoval dedukciu len za účinný spôsob rozbalenia dát, ktoré boli predtým prehľadne uschované vo všeobecných tvrdeniach. Dedukcia taktiež nie je len spôsob ako ospravedlniť tie presvedčenia, ktoré už máme. Sokrates uvažoval o dedukcii rovnako, ako my uvažujeme o experimente: ako o neutrálnej metóde, ktorá môže vyvrátiť aj tie naše názory, o ktorých sme najpevnejšie presvedčení.
Ako vidíme v jeho opise právnikov, Sokrates pohŕdal „zvláštnou obhajobou“, v ktorej sa najprv vyrukuje so záverom, a až potom sa prejednávajú dôvody pre prijatie takéhoto záveru. Propagandista sa snaží o hľadanie logického vysvetlenia len preto, aby vytvoril zdanie, že záver je rozumný. Sokrates si vedome nevšíma výsledky svojho zdôvodňovania, aby sa uistil, že bol vedený jedine predpokladmi a pravidlami usudzovania. Sokratovo sebaoslepenie nepochybne odkladá nabok informácie. Táto dohoda je nám však dobre známa vo forme double-blind (dvojnásobne slepých) experimentov, pri ktorých vedci predchádzajú uvažovaniu smerom k tomu, čo je želané, tým, že udržujú testované subjekty aj seba samých v nevedomosti ohľadom toho, kto dostáva účinné lieky a kto len placebo.
Keď povieme, že Zenónov úsudok o postupnom delení na polovicu „vyzerá zdravo“, myslíme tým len to, že vyzerá zdravo z určitej perspektívy – z perspektívy, ktorá nezahŕňa poznanie absurdnosti záveru. Stĺpy Partenónu vyzerajú ako rovné, ak sa ne pozeráme zo zeme, ale už sa tak nejavia zo strechy. Z výšky vidíme, že stĺpy sú prehnuté dovnútra, vďaka čomu môžu vyzerať ako rovné pre ľudí dolu. Keď Sokrates sleduje úsudok, kamkoľvek by viedol, odmieta zaujať takú perspektívu, ktorá berie do úvahy informácie o vierohodnosti záveru. Sokrates vždy usudzuje smerom dopredu vychádzajúc z predpokladov, nikdy nie odzadu zo záveru. (Jedinou výnimkou je jeho usudzovanie spôsobom reductio ad absurdum.) Aj dnes mnohí cítia, že filozof, ktorý sa spolieha na vonkajšiu evidenciu o závere je ako študent, ktorý nakúka do knihy s odpoveďami.
Veľa klamov vyžaduje špeciálne podmienky pozerania. Mám „nereálnu krabičku“ visiacu zo stropu v mojej kancelárii na neviditeľnej niti. Ak sa ma zvedavý návštevník spýta na tú nezvyčajne tvarovanú ozdobu, postavím ho na predurčenú vzdialenosť, poprosím ho, aby si zatvoril jedno oko a potom mu poviem, aby svoj pohľad zarovnal v smere pozdĺž blízkeho a vzdialeného rohu „krabičky“. Za týchto špeciálnych podmienok krabička vyzerá ako trojdimenzionálny ekvivalent obrázka 8.1. Veľa paradoxných úsudkov vyžaduje rovnako disciplinované hĺbanie. Namiesto toho, aby ste ich vyhodnocovali zvyčajným spôsobom, musíte začať od predpokladov, ktoré prijímate iba predbežne, ďalej pokračujte s pravidlami usudzovania a považujte ich za diskutabilný prevod, a potom potlačte nutkanie zabrzdiť pred cieľom cesty.
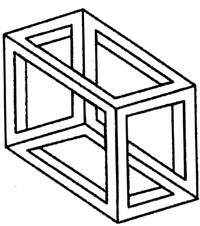
Obr. 8.1
Nikto neverí, že krabička je taká, ako vyzerá. Nikto to ani neočakáva. Pozorovatelia sa snažia sčasti pre samotný výjav a sčasti v nádeji, že sa poučia. Poznávacie paradoxy obsahujú rovnakú zmes estetickej a teoretickej príťažlivosti. Vedec, ktorý zažíva skreslenie pozorovania, ktoré je potrebné na to, aby mohol byť svedkom dvojitej dúhy, uzná, že dúhy sú ilúziami. Napriek tomu túto skúsenosť ocení rovnako ako pozorovanie skutočného fenoménu, akým je zatmenie slnka.
Problém protidôkazu
Významný odborník na Platóna Gregory Vlastos (1983) zvykol interpretovať Sokrata ako toho, kto vyvracal názory tých, čo s ním diskutovali, tak, že z nich odvodil protirečenie. Toto bol štandardný pohľad vyjadrený napríklad v Encyklopédii filozofie v hesle „dialektika“:
Sokratovský protidôkaz (elenchus) bol pravdepodobne vycibrenou formou zenónovských paradoxov, zdĺhavým krížovým výsluchom, ktorý vyvracia oponentovo pôvodné tvrdenie tým spôsobom, že ho prostredníctvom série otázok a odpovedí privádza k vyvodeniu dôsledkov, ktoré mu protirečia. Toto je logicky platný postup, pretože zodpovedá logickému zákonu: „ak z p vyplýva non-p, potom non-p je pravdivé“. (Hall 1967, 386)
Ale Vlastos napokon poznamenal, že Sokrates obyčajne dosiahol iba slabší výsledok: ukázal, že presvedčenia jeho partnera v dialógu sú ako celok nekonzistentné. Vlastos to pokladá za znepokojivé, pretože Sokrates má dojem, že vyvrátil konkrétny prvok nekonzistentnej množiny. Z logického hľadiska môže byť konzistencia znovunadobudnutá odmietnutím ktoréhokoľvek prvku množiny. Preto Sokrates vlastne nič nevyvrátil. Všetko, čo urobil, je, že ukázal, že jeho partner v dialógu potrebuje prehodnotiť niektoré zo svojich presvedčení.
Ba možno ani to nie! Správa o tom, že množina presvedčení je nekonzistentná, iba vtedy ospravedlňuje pátranie, ak existuje vyhliadka úspechu. Ak je v množstve pravdivých presvedčení ukrytých len niekoľko nepravdivých, potom je cena nápravy privysoká. Každé presvedčenie požíva vysokú mieru pravdepodobnosti. Za takýchto biednych podmienok pre pátranie sa zmierujeme s nekonzistenciou.
Sokrates v skutočnosti smeroval k zabezpečeniu toho, aby napokon prevládli dobré podmienky pre pátranie. Nekonzistencie odhalené Sokratom pozostávali z malej množiny presvedčení. Ďalej mali tendenciu k minimálnej nekonzistentnosti: eliminovanie čo i len jediného prvku množiny by stačilo na získanie konzistentnosti. Inak povedané presvedčenia v takomto malom priestore skúmania sú takmer konzistentné. Stačí sa v tom trochu povŕtať a problém môže byť vyriešený!
Sokrates nezamýšľal vytvoriť minimálne nekonzistentnú množinu. Jeho cieľom bolo odhaliť nekonzistenciu. Keď si myslel, že práca je hotová, prestal naliehať. Vedľajším produktom tejto dialektickej zdatnosti je to, že zanecháte nekonzistentného jedinca s nádejou, že sa stane konzistentným zmenou jediného presvedčenia.
Je protidôkaz neutrálny?
Sokrates koná tak, akoby protidôkaz bol univerzálnou metódou, ktorá mu umožní ujať sa všetkých príchodzích bez ohľadu na to, aké sú ich presvedčenia. Ale táto metóda má isté predpoklady. Po prvé, protidôkaz predpokladá, že sú prítomné nekonzistencie. Antisténes z Atén tvrdil, že žiaden výrok nemôže protirečiť inému výroku. K tejto myšlienke ho inšpiroval Parmenides: Výrok môže byť o Sokratovi, iba ak sa vzťahuje na Sokrata. Ak sa týka Sokrata, je to pravdivý výrok. Preto neexistuje žiaden nepravdivý výrok o Sokratovi. Výrok o Sokratovi môže byť popieraný iba vtedy, ak je možný nepravdivý výrok o Sokratovi. V dôsledku toho nie je možné poprieť žiaden výrok o Sokratovi. A čo platí pre Sokrata, platí pre všetky veci. Teda neexistujú žiadne protirečenia.
Zdá sa, že Platón sa zameral na Antisténa v dialógu Eutydemos. Antisténes je vykreslený ako prešibaný hašterivec zamestnaný praktikami, ktoré Protagoras propagoval ako „snahu o to, aby sa slabší argument zdal silnejším“. Antisténes na oplátku napísal polemiku proti Platónovi s neslušným názvom Sathon aleboČuráčik. Grécky výraz pre „čuráčika“ znie podobne ako „Platón“. Antisténes použil výraz Sathon na pomenovanie Platóna.
Protidôkaz, ktorý predpokladá protirečenia, nemôže byť pravdivý. Keďže si Antisténes myslí, že protirečenia neexistujú, súhlasí s tým, že neexistujú žiadne pravdivé protirečenia. Boli však aj takí filozofi, ktorí potvrdzovali oboje: existenciu protirečení aj ich pravdivosť. Príkladom zo súčasnosti je Graham Priest (1987). Myslí si, že menšina protirečení je pravdivá aj nepravdivá zároveň. Podľa Priesta paradoxy sa vyskytujú najmä v tejto provokatívnej menšine.
Priest si uvedomuje, že jeho stanovisko je v súčasnej klasickej logike neobhájiteľné. Ako sme videli pri negatívnom paradoxe striktnej implikácie, z nemožnosti vyplýva čokoľvek. Ak je nemožnosť striktným logickým protirečením, môžeme dokonca formálne odvodiť ľubovolný dôsledok: Z predpokladu p a non-pmôžeme vyvodiť p. Z p môžeme vyvodiť p alebo q (pričom q je akýkoľvek výrok). Teraz sa môžeme vrátiť kp a non-p a vyvodiť non-p. Ak non-p spojíme s predchádzajúcim výsledkom p alebo q, môžeme odvodiť q.
klasická logika je „výbušná“; z jediného protirečenia vyplýva každý výrok. Je nejaká možnosť, ako by sa Priest vyhol nekritickému akceptovaniu všetkého?
Ludwig Wittgenstein (1889 – 1951) si robil žarty z logikov, ktorí prehlasovali protirečenia za intelektuálnu pohromu. V skutočnom živote keď ľudia zistia, že upadli do protirečenia, bez ceremónií problém urovnajú – ak vôbec niečo urobia. Wittgenstein sa tešil na ten deň, kedy sa logici prispôsobia tejto antropologickej skutočnosti: „Vskutku, dokonca aj v tomto štádiu predpovedám čas, keď budú existovať matematické skúmania výpočtov, ktoré obsahujú protiklady, a ľudia budú vlastne hrdí na to, že sa oslobodili od konzistencie.“ (1964, 332)
A naozaj čoskoro nato povstali „dialethickí logici“. Pomenovali sa na základe Wittgensteinovej poznámky, že klamlivá veta je ako figúrka s hlavou boha Janusa otočená smerom k pravde aj k nepravde. (1978, IV.59) Dialetheia [12] je dvojaká pravda. Graham Priest ako dialethik oceňuje konzistenciu, ale iba relatívne, keď oceňuje jednoduchosť, všeobecnosť, a empirickú úspešnosť. Konzistentnosť je iba jedným z mnohých žiadúcich znakov. V prípade paradoxu klamára si Priest myslí, že by sme mali vymeniť trochu konzistencie, aby sme tak získali viac jednoduchosti. Konkrétne by sme mali uznať, že veta „Táto veta nie je pravdivá“ je pravdivá aj nepravdivá zároveň, a potom by sme mali použiť „parakonzistentnú logiku“, aby sme zabránili ďalšiemu šíreniu protirečenia.
Parakonzistentná logika je navrhnutá tak, aby zabezpečila spútanie explózie. Napríklad sa v nej odmieta pravidlo usudzovania „p, a preto p alebo q“ na základe toho, že platný úsudok musí mať predpoklady, ktoré sú relevantné vo vzťahu k záveru. Spomínaní logici rozšírili túto požiadavku relevancie na kondicionály v snahe predísť paradoxom implikácie.
Dialethici prezentujú seba samých ako priateľov protirečení. Pripomínajú mi farmárov, ktorí prezentujú seba samých ako priateľov koní, ktorých kastrujú. Valach [13] nie je nejakým krotkejším druhom žrebca, on vôbec nie je žrebcom. Protirečenia dialethikov môžu vyzerať a vyznievať ako protirečenia, ale nemôžu zohrávať tú rolu, ktorá je podstatná pre to, aby boli skutočnými protirečeniami; nemôžu slúžiť ako rozhodujúci koncový bod postupu reductio ad absurdum. Prinajlepšom môžu byť výrokom q v úsudkumodus tollens: Ak p, tak q; non-q, a preto non-p. Takže nakoniec si myslím, že Priest upadol do Antisténovho skepticizmu týkajúceho sa protirečení.
Či už so mnou Priest súhlasí vo veci jeho skeptickej spriaznenosti s Antisténom alebo nie, mal by súhlasiť v tom, že úsudky typu hromada spôsobujú problém pre Sainsburyho definíciu paradoxu. Bol som totiž opatrný pri subjektivizovaní mojich príkladov. Zdôvodňovanie v úsudkoch typu hromada bude prijateľné pre tých, ktorí veria v klasickú logiku. Aj napriek tomu, že moje zdôvodňovanie v úsudku typu hromada je neprijateľné pre Grahama Priesta, ten bude správne počítať s tým, že toto zdôvodňovanie je prijateľné pre mňa – a väčšinu logikov. Takže podľa Sainsburyho definície by som mal úsudky typu hromada považovať za paradoxy. Ale keďže úsudky typu hromada nie sú skutočnými paradoxmi, ukazujú, že Sainsburyho definícia je príliš široká.
P o z n á m k y
[1] Ang. slovo „reasoning“, ktoré prekladám ako zdôvodnenie, tu má špecifický význam a znamená postupnosť presne vyargumentovateľných krokov, ktoré vedú od predpokladov k záveru.
[2] Etymológia mena Aristokles býva častejšie interpretovaná inak: Αριστοκλής (άριστος + κλέος) ο έχων άριστη δόξα (http://www.zosimaia.gr/arts.asp?maintext=ar-erri, 22. 7. 2005), čo znamená „majúci najlepšiu povesť“, prípadne „majúci najlepšiu mienku“ alebo jednoducho „najslávnejší“.
[3] Konzistentný z hľadiska logiky je taký, ktorý nie je v rozpore sám so sebou alebo nevedie k rozporu. Preto konzistentne priradiť znamená priradiť tak, že to napokon nepovedie k rozporu.
[4] Ang. slovo „belief“ prekladám ako presvedčenie. Slovenské slovo viera má skôr náboženské konotácie, preto jeho použitie by v tomto prípade bolo zavádzajúce. Ang. sloveso „to believe“ prekladám väčšinou ako domnievať sa a „believer“ ako vyznavač (teda ten kto vyznáva nejaké presvedčenie).
[5] Použil som slovenský preklad: Platón: Teaitetos 170 A, In: Platón: Dialógy II. Tatran, Bratislava 1990, s. 464.
[6] Aj tu som použil slovenský preklad: Platón: Teaitetos 170 A-B, In: Platón: Dialógy II. Tatran, Bratislava 1990, s. 464. Anglický preklad sa od slovenského trochu odlišuje, navyše autor uvádza posunuté „súradnice“: Teaitetos 170 B-C.
[7] V slovenčine sa bežnejšie používa „logický správny úsudok“, ale tu budem „valid argument“ prekladať ako platný úsudok.
[8] Autor má na mysli významných predstaviteľov megarsko-stoickej školy Euklida z Megary (Sokratov žiak, ktorý žil okolo r. 400 p. n. l.) a Filóna z Megary (ako prvý analyzoval implikáciu a žil okolo r. 300 p. n. l.).
[9] Tu autor použil gramatický popis, inde hovorí o implikácii, to je bežné označenie kondicionálu ako logickej spojky.
[10] Teda v zmysle striktnej implikácie.
[11] Sorites je grécke slovo, ktoré sa zaužívalo pre označenie paradoxu hromady. (Keď pridám k zrnkám piesku jedno zrnko, hromada z toho nebude. Ale keď ich pridám toľko, koľko ich vytvára hromadu, bude to ešte platiť? Ktoré zrnko spôsobilo vznik hromady?) Pozri GAHÉR, F.: Logika pre každého. Bratislava : Iris 2003, 3. doplnené vydanie, s. 379-380, tiež http://plato.stanford.edu/entries/sorites-paradox/.
[12] Aletheia je grécky výraz pre pravdu, doslova znamená odkrytosť. Dialetheia je novotvar, slovná hračka, ktorá znamená niečo ako „dvojpravda“.
[13] Vykastrovaný žrebec.
Z 8. kapitoly knihy Sorensen, Roy: A Brief History of the Paradox. Philosophy and the Labyrinths of the Mind. Oxford University Press, New York 2003, s. 100 – 115, preložili Reginald A. Slavkovkovský a Michal Kukučka.